En muchas aplicaciones en las que se relaciona la informática, es crucial gestionar los datos para realizar operaciones de búsqueda, inserción y eliminación de nodos. Donde los árboles ayudan mucho a facilitar este proceso, sin embargo, un arbol binario de búsqueda convencional puede quedar bastante corto debido a las limitaciones de este especialmente cuando la inserción de los datos no se hace de manera uniforme o de entradas muy grandes, lo que empeorara y hará que la estructura pueda a llegar un orden de complejidad, lo que provocara un bajo rendimiento, un gran consumo de memoria y volverse ineficaz a largo plazo.
Es por eso por lo que el uso de árboles AVL es esencial para realizar operaciones de búsqueda, inserción y eliminación donde el conjunto de datos es dinámico y cambiante, por ello es importante conocer mas acerca de estas estructuras y el como se pueden usar de manera eficaz y optimizada.
Objetivos de Arbol AVL
1. Describir de manera general de lo que es exactamente un Arbol AVL y todo referente a ello.
2. Que utilidad tienen los arboles AVL en la estructura de datos.
3. Analizar las diferentes ventajas y desventajas que tiene el uso de una estructura de árboles AVL.
¿Qué es?
Un árbol AVL es un árbol de búsqueda binario tal que, para cualquier nodo en el árbol, la altura de la izquierda y los subárboles derechos pueden diferir como máximo en 1.
¿Para qué sirve?
El propósito principal de un árbol AVL es garantizar que las operaciones de búsqueda, inserción y eliminación se realicen en tiempo logarítmico. Esto lo convierte en una estructura muy útil en aplicaciones que requieren eficiencia en la manipulación de grandes cantidades de datos. Los árboles AVL son utilizados en bases de datos, sistemas de archivos, y en cualquier contexto donde sea crucial mantener datos ordenados y garantizar un acceso rápido a ellos.
¿Cómo funciona?
El árbol AVL funciona asegurando que la diferencia de altura entre el subárbol izquierdo y el subárbol derecho de cada nodo (llamada factor de equilibrio) no sea mayor que 1 ni menor que -1. Si el árbol pierde este equilibrio después de una inserción o eliminación, se realizan rotaciones para restaurar el balance.
Operaciones con árboles AVL
Las operaciones en los árboles AVL corresponden y son similares a las de un árbol binario; entre ellas están:
- Insertar
- Eliminar
- Buscar
Se debe tener en cuenta que, al momento de insertar o borrar, se comprueba si el árbol está equilibrado; en caso de no estarlo, se realiza el balanceo.
Rotaciones
Las rotaciones son el único método que se utiliza para balancear un árbol AVL.
Estas se desglosan en 4 variaciones, las cuales son:
- Rotación Simple a la derecha (RSD)
- Rotación Simple a la Izquierda (RSI)
- Rotación Doble a la Derecha (RDD)
- Rotación Doble a la Izquierda (RDI)
Factor de equilibro
Reestructurar el árbol significa rotar sus nodos y para que la rotación se efectúe se requiere de un factor de equilibro (FE o balance), el cual se define como la diferencia entre las aturas del subárbol derecho y el subárbol izquierdo.
FE = altura subárbol derecho – altura de subárbol izquierdo
Nota: para que sea un árbol AVL, estos valores deben ser 1, 0, -1:
-1: cargado a la izquierda
0: equilibrado
1: cargado a la derecha
Rotación simple a la izquierda
Esta rotación se utiliza cuando el subárbol izquierdo de un nodo sea 2 unidades más alto que el derecho, en otras palabras, cuando el FE sea de -2 y, además, la raíz del subárbol izquierdo tenga un FE de -1, es decir, que esté cargado a la izquierda.
Rotación simple a la derecha
Esta rotación se utiliza cuando el subárbol derecho de un nodo sea 2 unidades más alto que el izquierdo, en otras palabras, cuando el FE sea de 2 y, además, la raíz del subárbol derecho tenga un FE de 1, es decir, que esté cargado a la derecha.
Rotación doble a la derecha
Conocida también como rotación derecha-izquierda. Si está desequilibrado a la izquierda (FE > +1) y su hijo derecho tiene distinto signo (-), se realiza rotación doble a la derecha.
Rotación Doble Derecha = Rotación Simple Derecha + Rotación Simple Izquierda
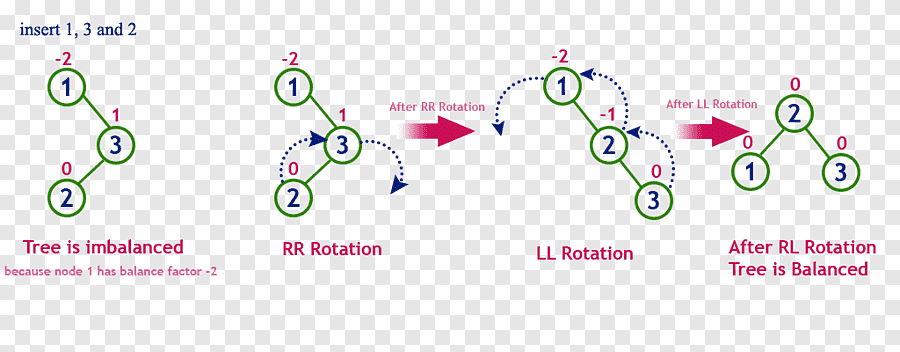
Rotación doble a la izquierda
Rotación izquierda-derecha
Si está desequilibrado a la derecha (FE < -1) y su hijo izquierdo tiene distinto signo (+), se realiza rotación doble a la izquierda.
Rotación Doble Izquierda = Rotación Simple Izquierda + Rotación Simple Derecha
Utilidad de los Árboles AVL en la estructura de datos
Los árboles AVL son útiles en estructuras de datos porque garantizan que las operaciones de búsqueda, inserción y eliminación se realicen de manera eficiente en O(log n) al mantener el árbol siempre balanceado, lo que los hace ideales para manejar grandes volúmenes de datos en sistemas donde la velocidad y el acceso rápido son esenciales, como bases de datos, sistemas de archivos y algoritmos dinámicos.
Ventajas del Árbol AVL
1. Eficiencia en operaciones: Las operaciones de búsqueda, inserción y eliminación son todas O(log n), garantizando un acceso eficiente a los datos.
2. Balance automático: Siempre garantiza que el árbol esté equilibrado, lo que minimiza la posibilidad de que las operaciones se vuelvan ineficientes.
3. Adecuado para grandes conjuntos de datos: Es ideal cuando se trabaja con grandes volúmenes de datos que necesitan ser accedidos o modificados frecuentemente.
4. Fiabilidad en la búsqueda: Ofrece tiempos consistentes de búsqueda, incluso en el peor de los casos.
Desventajas del Árbol AVL
1. Sobrecarga de rotaciones: Después de algunas operaciones (especialmente inserciones y eliminaciones), puede requerir varias rotaciones, lo que añade complejidad y sobrecarga en comparación con un simple árbol binario de búsqueda.
2. Complejidad de implementación: Implementar un árbol AVL es más complicado que un árbol binario de búsqueda ordinario, debido a la necesidad de mantener el balance y realizar rotaciones.
3. Mayor uso de memoria: Cada nodo necesita almacenar información adicional (como la altura del nodo o el factor de equilibrio), lo que incrementa el consumo de memoria.
Ejemplos de Aplicaciones de Árboles AVL
1. Sistemas de bases de datos: Utilizados para indexar claves de búsqueda y mantener las operaciones eficientes.
2. Compiladores: Los árboles AVL pueden utilizarse en el análisis sintáctico de expresiones.
3. Redes: Se utilizan en algoritmos de enrutamiento para mantener una estructura jerárquica equilibrada.
4. Sistemas de archivos: Ayudan a organizar y acceder a archivos grandes de forma eficiente.
BIBLIOGRAFIA
Hernández Bejarano, M., Baquero Rey, L. E. (2021). Estructuras de datos: fundamentación práctica. Ediciones de la U. https://www-ebooks7-24-com.unipiloto.basesdedatosezproxy.com/?il=16014
Franco, E. (2017). Árbol Balanceado AVL. IPN Escuela Superior de Computo. Obtenido de: https://docencia.eafranco.com/materiales/estructurasdedatos/11/Tema11.pdf
Master, H. (2016). ARBOLES AVL. Estructuras Unincca. Obtenido de: https://structurasunincca.blogspot.com/2016/03/arboles-avl.html